Algorithmik (Vorlesung 1)

In der ersten Vorlesung von Algorithmik haben wir die Ziele der Vorlesung besprochen und Grundbegriffe anhand von einfachen Algorithmen diskutiert.

Anfang	algo_teil01_1 – Seite 1
Ende	algo_teil01_2 – Seite 18

---

Allgemeines

Begrifflichkeiten

• Wert einer Teilzahlenfolge: \(w(a, i, k)=\sum_{j=i}^{k}a[j]\)
• i = Kleinster Index
• k = Höchster Index
• n = Länge der Zahlenfolge
• Es gilt, dass die Werte von i und k nicht größer als n sein können
• Der Wert i darf nicht größer sein als k
• 1 ≤ i ≤ k ≤ n
• T(n) ist die Anzahl der Additionen und Vergleiche

Beispielhafte Anwendung\( \ a = 3, -5, 7, 2, -1 \ w(a,1,3) = +3-5+7 = 5 \ w(a,2,4) = -5+7+2 = 4 \ \)

Analyse von Algorithmen

Zielstellung

• Einen effizienten Algorithmus zur Bestimmung der größten Teilfolge einer n-elementigen Folge bestimmen

Algorithmus 1

Vereinfachte Berechnung/Darstellung über eine Tabelle

w(a, i, k)	k = 1	k = 2	k = 3	k = 4	k = 5
i = 1	3	-2	5	7	6
i = 2	–	-5	2	4	3
i = 3	–		7	9	8
i = 4	–	–	–	2	1
i = 5	–	–	–	–	-1

Welche Operationen werden angewandt?

• Additionsoperation +
• Vergleichsoperation =

Wie oft muss addiert werden?

• Es gibt 10 Additionsoperation (vgl. Tabelle)
• Hierbei wird ausgenutzt, dass man die vorherigen Summen weiterverwenden kann: \(w(a,i,k+1) = w(a,i,k) + a[k+1]\)

w(a, i, k)	k = 1	k = 2	k = 3	k = 4	k = 5
i = 1	0	1	1	1	1
i = 2	–	0	1	1	1
i = 3	–		0	1	1
i = 4	–	–	–	0	1
i = 5	–	–	–	–	0

Wie oft muss verglichen werden?

• Für jede erzeugte Folge (15 Stk.) muss einmal verglichen werden, außer für die Erste
• Daher ergibt sich: 15 – 1 = 14 Vergleichsoperation

Wie sieht ein Algorithmus zur allgemeinen Bestimmung der Additionen aus?

• Erste Überlegung: \(A(n) = (n-1)+(n-2)+…+1 = \sum_{n-1}^{i=1}i=\frac{n*(n-1)}{2}\)

Wie kann dies grafisch hergeleitet werden?

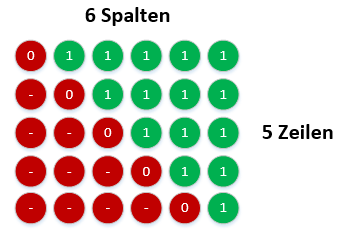
• Es gibt n-1 Zeilen und n Spalten
• Aber nur die Hälfte davon hat Additionen (grüner Bereich)
• Daraus ergibt sich \( \frac{n*(n-1)}{2} \)

Wie sieht die Überlegung zu Vergleichsoperationen aus?

• Für jede Zelle muss verglichen werden, außer beim ersten Mal
• Daraus ergibt sich: \(V(n) = n+(n-1)+(n-2)+…-1=\sum_{n}^{i=1}\frac{n*(n+1)}{2}-1 \)

Wie viele Operationen werden nun benötigt?

• \(T(n)=A(n)+V(n) = n^2 -1\)
• Ohne den Trick würde die Summe aller Operationen circa n³ betragen

Algorithmus 2

Wie viele Operationen werden nun benötigt?

• Das maximale Element ist in der linken Teilsumme: \(z_1 = w_{max}(a,1,m)\)
• Das maximale Element ist in der rechten Teilsumme: \(z_2 = w_{max}(a,m+1,n)\)
• Das maximale Element beginnt in der linken Teilsumme und endet in der Rechten: \(z_{3} = z_{3}‘ + z_{3}“\)
• \(z = max(z1, z_2, z_3)\)

Was sind \( z_{3}’\) und \( z_{3}“\)?

• \( z_{3}’\) entspricht \(w_{rechts}(a,1,m)\) mit einem fixem Wert für m
• \( z_{3}“\) entspricht \(w_{links}(a,m+1,n)\) mit einem fixem Wert für m+1
• \(w_{max}(a,1,m)\) ist ungleich \(w_{rechts}(a,1,m)\)

Ein Beispiel für \( z_{3}’\): n = 8

• \( z_{3}^{‚} = w_{rechts}(a,1,4) = max(w(a,1,4), w(a,2,4), w(a,3,4), w(a,4,4))\)

Wie viele Additionen benötigt man für wrechts(a,1,m)?

• Es werden n-1 Additionen benötigt
• \(w_{rechts}(a,1,4)\) benötigt somit 3 Additionen

Wie viele Operationen werden insgesamt benötigt?

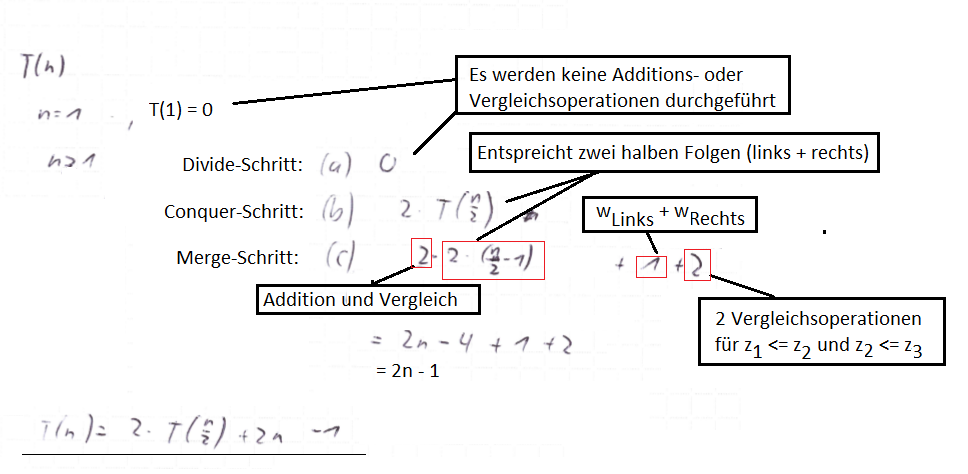
Anzahl der Operationen am Beispiel: n=2³

Algorithmus 3

Einleitung zu Sweep-Line bzw. Scan-Line

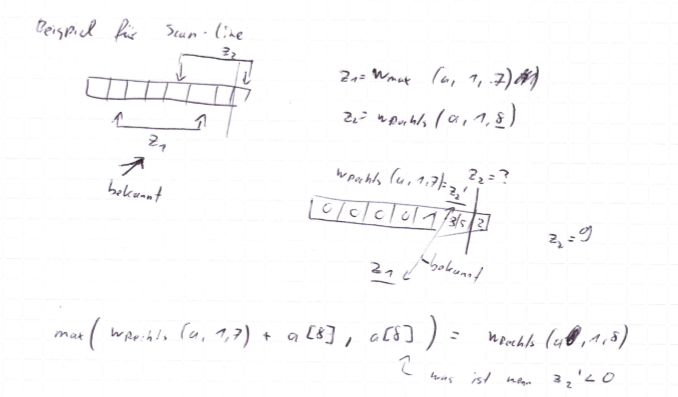
Beispiel zu Sweep-Line: a = 3, 2, -1, 5, -3

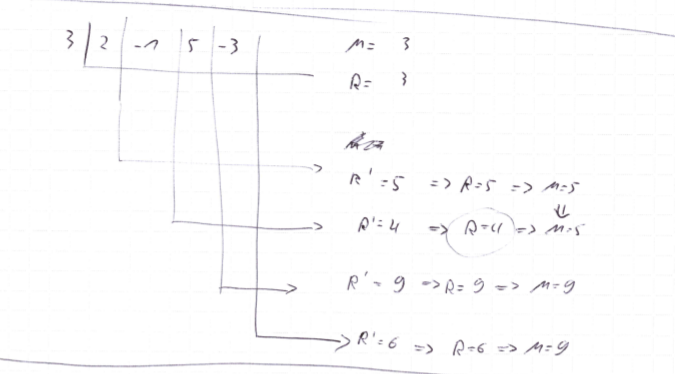
Wie viele Operationen werden benötigt?

Beurteilung der Laufzeit von Algorithmen

Einleitung

• Die vorherigen Algorithmen hatten eine von der Eingabe unabhängige Laufzeit
• Etabliert ist, dass man den Vergleich am worst case durchführt
• Eine Bestimmung vom average case ist nicht immer möglich
• Der average case orientiert sich an einem gleichverteilten Erwartungswert von \( \frac{1}{\text{Eingaben } E_n} \)

Beispiel: Kosten für eine Sortierfunktion

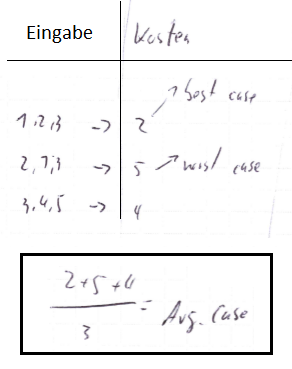
Beispiel: Erzeugung von Binärzahlen

• Es kommen 1, 2, n oder n + 1 Bitänderungen vor
• Der worst case entspricht: n + 1

\( \ 000 \rightarrow 001 \text{ (1 Bit = n – 2 Bit)} \ 001 \rightarrow 010 \text{ (2 Bit = n – 1 Bit)} \ 010 \rightarrow 011 \text{ (1 Bit = n – 2 Bit)} \ 011 \rightarrow 100 \text{ (3 Bit = n Bit)} \ 100 \rightarrow 101 \text{ (1 Bit = n – 2 Bit)} \ 101 \rightarrow 110 \text{ (2 Bit = n – 1 Bit)} \ 110 \rightarrow 111 \text{ (1 Bit = n – 2 Bit)} \ 111 \rightarrow 1000 \text{ (4 Bit = n + 1 Bit)}\)

Wie oft tritt dies bei einer Binärzahl der Länge n auf?

• 1 Bit: 2^n-1 (‚0‘ hinten)
• 2 Bit: 2^n-2 (’01‘ hinten)
• n Bit: 2⁰ = 1
• n+1 Bit: 2⁰ (Alles ‚1‘) = 1

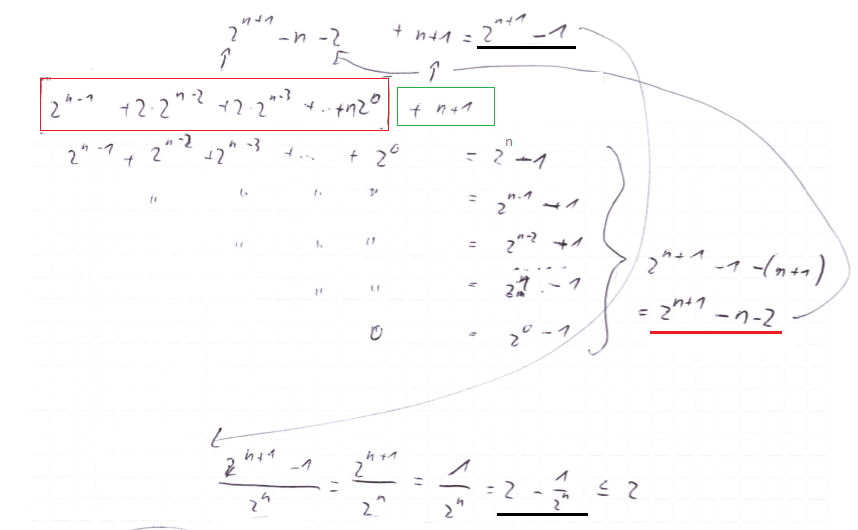
Beispiel: Schranken für n⁵